*buddel buddel*
Wollte keinen neuen Thread aufmachen, das dieser hier auch tut.
Ich wurde vor kurzem gefragt, wies so mit Statistik und den beiden Würfelmethoden aussieht... Tja, also habe ich mich mal hingehockt und eine kleine Simulation geschrieben *g*
(Die Simulation wird mit dem Programm Matlab für >>n<< "Messreihen" durchgeführt; ich habe 100000 genommen).
Was kann die Simulation?
Es werden (in unterschiedlichen Scripts) beide Würfelmethoden (Beste von 2 für jeden Wert, sofort zuteilen - kurz 12W; die 6 besten aus 9 - kurz 9W) simuliert und je 3 Histogramme erzeugt. Dabei wird die Minimalwertesumme von 350 berücksichtigt. Das erste Histogramm ist logischerweise der (arithmetische) Mittelwert (Summe/6). Die beiden anderen sind Primär- und Sekundärattribut des gewünschten Charakters. Für den 9er Wurf ist das natürlich sehr einfach, da einfach die beiden höchsten Werte genommen wurden.
Beim 12er Wurf musste ich etwas "tricksen". Das Primärattribut wird "zufällig" aus den besten beiden Werten genommen, das Sekundärattribut aus den besten 4, wobei 2 und 3 den Fokus haben (Wahrscheinlichkeit: je 16,6% 1 und 4, je 33,3% 2 und 3); natürlich kann in jeder Messreihe das Primärattribut nicht gleichzeitig das Sekundärattribut sein.
Kommen wir zur Auswertung auf 100.000 "Messungen":
Die Plots wurden mit OriginPro 8 erstellt.
[PRBREAK][/PRBREAK]
Mittelwert
9er Wurf:
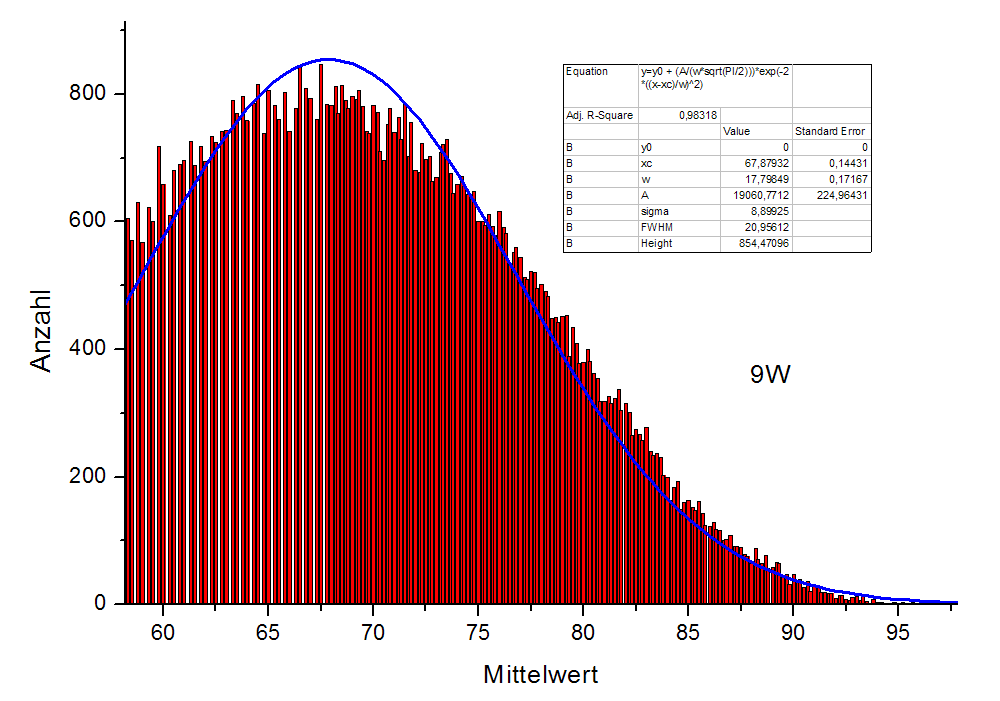
12er Wurf:
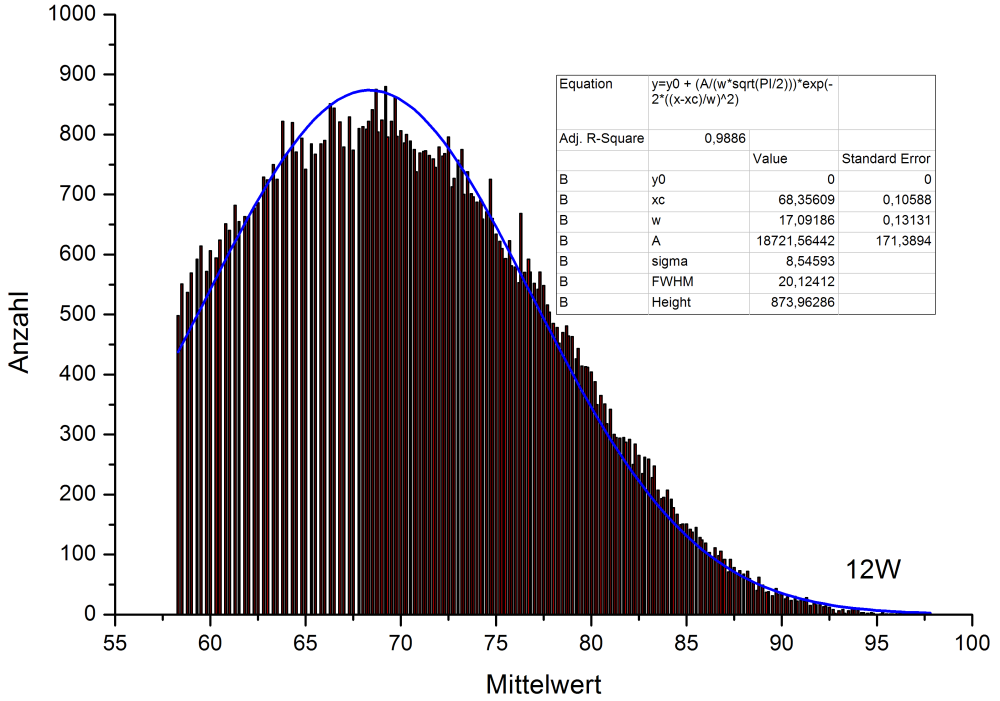
Was hier auffällt (am Orginal sieht mans natürlich besser), ist dass einige Werte verboten sind - und zwar im unteren Teil mehr als im oberen.
Unterhalb von 68 (Mittelwert) sind für die 1. Dezimalstelle nur 0,3,5,8 zulässig.
Oberhalb von 68 0,2,3,5,7,8
Der Grund hat etwas mit dem durch 6 teilen bei der Bildung des Mittelwerts zu tun. Aber ich bin zu faul, mathematisch zu begründen, warum nur diese Stellen zugelassen werden....
Die Histogramme wurden mit einem Gauß gefittet.
Der Mittelwert ist beim 12W etwas höher (um etwa 0,5), dafür ist dort die Peakbreite etwas kleiner (um 0,7).
Da das FWHM (Full Width at Half Maximum) auf der linken Seite schon im "verbotenen" Bereich liegt spielt es eigentlich keine Rolle für den Mittelwert. Mit der 12W Methode bekommt man im Mittel einen minimal größeren Mittelwert (was nen Satz...), dafür ist beim 9W die Chance auf einen etwas größeren Mittelwert minimal größer (die Chance auf einen schlechteren Wert wird großteils durch den Cut bei 58,3 ausgeglichen).
Primärattribut
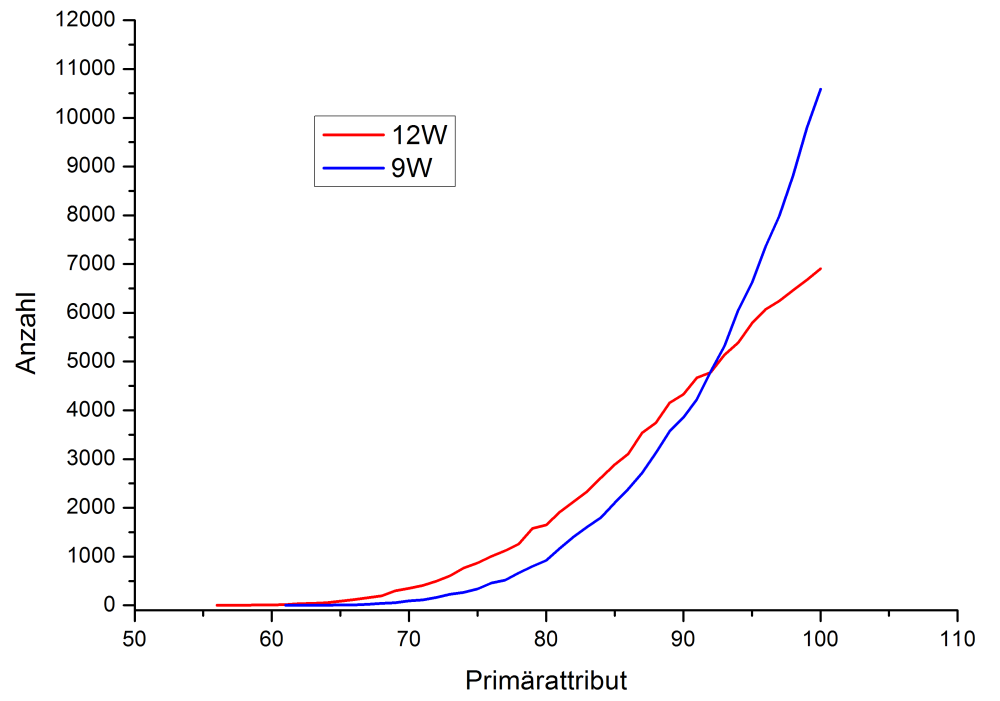
Hier gibt es nichts besonderes: natürlich hat man im 9er Wurf immer den besten Wert zur Verfügung. Etwas genauer:
in 44,5% der Fälle hat man beim 9er Wurf einen Wert von 96 oder Höher. In immerhin noch 30,9% zwischen 90 und 95.
Im Vergleich beim 12W: 32,3% (96-100) und 30% (90-95)
Sekundärattribut
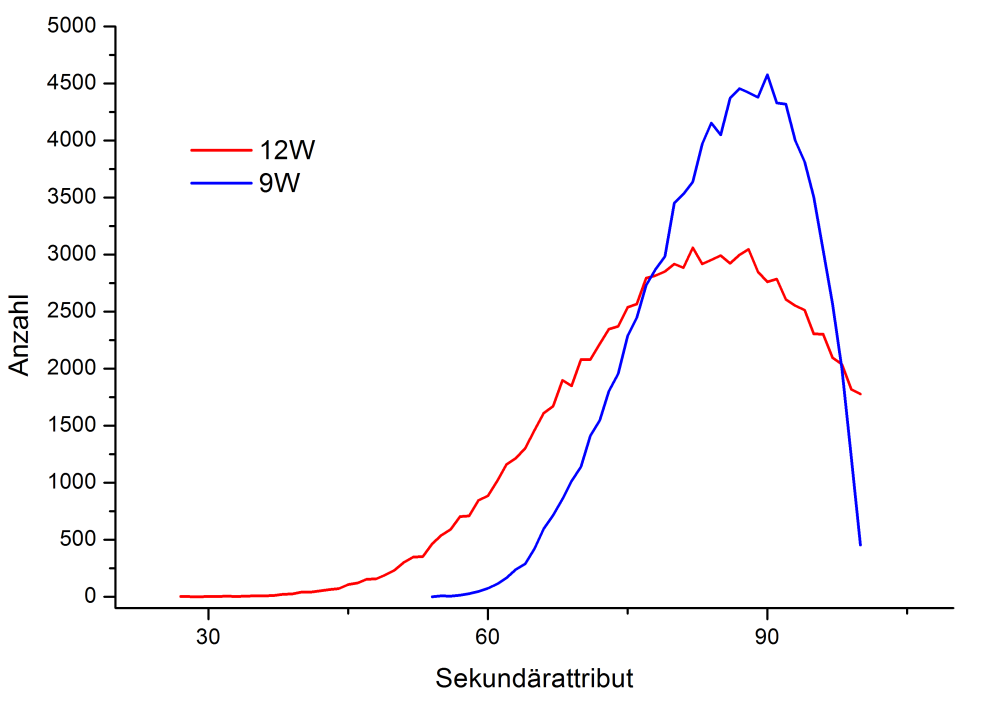
Auch hier: der verlauf ist nicht weiter verwunderlich. Allgemein sind die Sekundärattribute beim 9W höher.
Wie sieht es mit den Wahrscheinlichkeiten aus, einen Wert in den Bereichen 90-95 bzw. 96-100 zu haben?
Für den 9er Wurf: 24,5% (90-95) und 9,2% (96-100)
Für den 12er Wurf: 15,5% (90-95) und 10% (96-100)
Hier kann man schon eine Tendenz erkennen: Ein Tertiärattribut wird wahrscheinlich beim 12er Wurf schon besser ausfallen.
Ein etwas ausgefeilteres System (programmiertechnisch etwas aufwändig. Man müsste wirklich für jeden Wurf eine ganze Auswahl an Select Anweisungen machen, dann könnte man das ganze besser simulieren. Z.B. würde jeder Spieler bei einem 1. Wurf ab 96 als Primärattribut setzen) für den 12W würde die Prozentsätze etwas anheben, insbesondere für das Sekundärattribut. Ich würde mir für ein etwas intelligenteres System einen Zuwachs von je 2% für das Primärattribut bzw. 5% für das Sekundärattribut erwarten.
Schauen wir uns noch kurz die Wahrscheinlichkeit an, dass beide Attribute in einem gewissen Bereich sind:
9W:
Primärattribut und Sekundärattribut in 96-100: 4,1%
Primärattribut aus 96+, Sekundärattribut aus 90-95: 10,9%
Primärattribut aus 96+, Sekundärattribut unter 90: 29,5%
Primärattribut und Sekundärattribut aus 90-95: 7,6%
Primärattribut aus 90-95, Sekundärattribut unter 90: 20,5%
Beide unter 90: 24,6%
(Summe etwas unter 100% => Rundungsfehler)
12W:
Primärattribut und Sekundärattribut in 96-100: 3,23%
Primärattribut aus 96+, Sekundärattribut aus 90-95: 5%
Primärattribut aus 96+, Sekundärattribut unter 90: 24,06%
Primärattribut und Sekundärattribut aus 90-95: 4,65%
Primärattribut aus 90-95 und Sekundärattribut aus 96+: 3%
Primärattribut aus 90-95, Sekundärattribut unter 90: 22,35%
Primärattribut aus unter 90, Sekundärattribut aus 96+: 3,77%
Primärattribut unter 90, Sekundärattribut aus 90-95: 4,65%
Beide unter 90: 28,09%
(Summe etwas unter 100% => Rundungsfehler)
Fazit: Ich müsste das ganze noch mit einem Tertiärattribut und einem besseren System für die Wertzuteilung beim 12W arbeiten.
Ich würde jetzt schätzen, dass bei einem Charakter, der auf 3 Attributen basiert (Kampfzauberer vor allem) der 12W bessere Charaktere liefern kann, wohingegen der 9W definitiv für 2 Attributcharatere (hauptsächlich alle reinen Zauberer) besser geeignet ist.
Sollte wer Fehler finden (*zu Solwac schiel*) - bitte melden!






Empfohlene Kommentare
Nimm an der Diskussion teil
Du kannst jetzt einen Beitrag schreiben und dich später registrieren. Wenn du bereits ein Konto hast, melde dich an, um den Beitrag über dein Konto zu veröffentlichen.